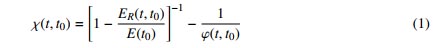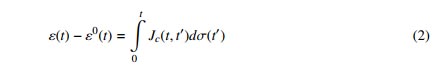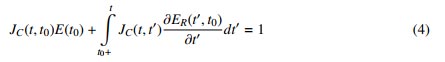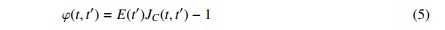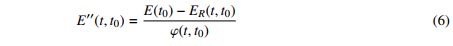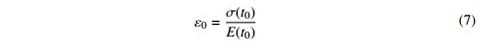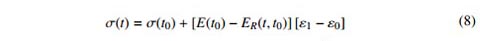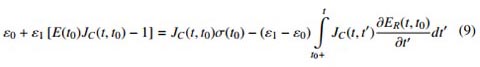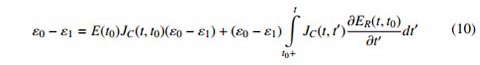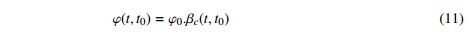Nội dung bài báo trình bày tính toán độ võng dài hạn của dầm BTCT khi xét đến ảnh hưởng của sự già hóa của bê tông với hai nội dung chính: (1) xây dựng mối quan hệ giữa hệ số từ biến và hệ số già dựa trên đề xuất của Bazant cho bê tông có các cấp cường độ nén khác nhau; (2) tính toán độ võng dài hạn có xét đến sự già hóa dựa trên mô hình Mô đun đàn hồi hiệu quả có điều chỉnh (AEMM). Các kết quả tính toán sẽ được so sánh với kết quả thực nghiệm, từ đó sẽ cho thấy rõ mức độ ảnh hưởng khi không xét và có xét tới sự già hóa của bê tông đến độ võng dài hạn của dầm.
1. Đặt vấn đề
Kết cấu dầm bê tông cốt thép (BTCT) là loại kết cấu được sử dụng rộng rãi nhất hiện nay trên các công trình xây dựng. Đối với kết cấu này, sự làm việc của chúng phải thỏa mãn các điều kiện liên quan đến các trạng thái giới hạn về cường độ (trạng thái giới hạn thứ 1 - TTGH 1) và trạng thái giới hạn về điều kiện sử dụng (trạng thái giới hạn thứ 2 - TTGH 2). Việc tính toán theo TTGH 1 nhằm đảm bảo cho kết cấu không bị phá hoại, không bị mất ổn định dưới tác dụng của tải trọng. Tính toán theo TTGH 2 đảm bảo cho kết cấu BTCT làm việc bình thường kể từ khi kết cấu bắt đầu chịu tác dụng của tải trọng. Đối với kết cấu dầm BTCT, điều này được thực hiện thông qua việc tính toán nhằm đảm bảo không xuất hiện trên kết cấu những khe nứt hoặc những biến dạng (độ võng) vượt quá giá trị cho phép (thường lấy theo quy định trong các tiêu chuẩn thiết kế hiện hành).
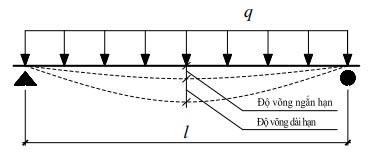
Hình 1. Các thành phần độ võng của dầm theo thời gian.
Trong việc tính toán theo TTGH 2 thì tính toán khống chế độ võng được đề cập đến trong các tiêu chuẩn thiết kế. Độ võng của kết cấu BTCT chịu uốn bao gồm hai thành phần là độ võng ngắn hạn (độ võng tức thời) và độ võng dài hạn, Hình 1. Độ võng ngắn hạn được tính toán dựa trên tác dụng tức thời của tải trọng (ví dụ độ võng tại thời điểm dỡ cốp pha, cột chống hoặc độ võng do có sự gia tăng của tải trọng tác dụng. Độ võng dài hạn của kết cấu dầm BTCT xảy ra khi kết cấu chịu tác dụng của tải trọng duy trì theo thời gian và độ võng này cũng tăng dần theo thời gian tác dụng tải trọng. Nhiều tài liệu nghiên cứu [1-18] cho thấy thành phần dài hạn của độ võng có thể lớn gấp từ 2 - 3 lần độ võng tức thời. Độ võng dài hạn của kết cấu dầm BTCT là một quá trình phức tạp và gắn liền với các đặc tính biến dạng dài hạn của vật liệu bê tông như biến dạng co ngót, biến dạng từ biến, biến dạng nhiệt.
Việc tính toán thiết kế kết cấu công trình BTCT theo TTGH 2 nói chung và đối với kết cấu dầm BTCT chịu uốn nói riêng đã được trình bày kỹ càng trong một số tiêu chuẩn thiết kế hiện nay như tiêu chuẩn Châu Âu Eurocode 2 (EC2) [1], tiêu chuẩn Hoa Kỳ ACI 318-14 [2], tiêu chuẩn Việt Nam TCVN 5574:2018 [3]... Một đặc điểm chung của các công thức tính độ võng dài hạn trong các tiêu chuẩn là sử dụng rất nhiều các hệ số thực nghiệm liên quan đến cấp phối vật liệu chế tạo, điều kiện bảo dưỡng, thời gian tác dụng của tải trọng... Các thông số đặc trưng cho sự làm việc dài hạn của bê tông được kể đến trong tính toán gồm biến dạng từ biến, biến dạng co ngót của vật liệu này.
Do đặc điểm cấu trúc của vật liệu bê tông, khi bê tông làm việc dài hạn, chịu tác dụng của tải trọng và các yếu tố tác động khác, cấu trúc của bê tông có sự thay đổi nhất định. Đặc điểm này thường gắn với tên gọi “sự già hóa” của bê tông theo thời gian và một số nghiên cứu đã chứng minh, đặc trưng này của bê tông có ảnh hưởng đến ứng xử dài hạn của bản thân bê tông và của kết cấu BTCT.
Carlswärd [4] và Westman [5] giải thích sự ảnh hưởng của sự già hóa là kết quả của quá trình hydrat hóa liên tục của gel xi măng khi bê tông được chất tải ở độ tuổi sớm. Ở độ tuổi sớm, gel xi măng có sẵn mang theo tất cả ứng suất, nhưng khi quá trình hydrat hóa tiếp tục, gel mới được hình thành làm giảm ứng suất cho gel xi măng ban đầu.
Tính toán sự làm việc dài hạn của kết cấu BTCT có kể đến hệ số già đã được một số tác giả đề cập đến, điển hình như các nghiên cứu [6-8]. Trong đó, sự già hóa của bê tông thường được kể đến thông qua hệ số già (ageing coefficient) ký hiệu là χ(t; t0). Bazant [6, 7] đã kể đến ảnh hưởng của hệ số già qua việc đưa hệ số này vào trong công thức xác định mô đun đàn hồi của bê tông, còn được gọi bằng phương pháp mô đun đàn hồi hiệu quả có điều chỉnh theo tuổi (Age-adjusted effective modulus method - AEMM). Theo đó, hệ số già được xác định trên cơ sở hệ số từ biến của bê tông và là một hàm số của thời gian.
Có thể thấy rằng sự già hóa của bê tông biểu diễn thông qua hệ số già đã được nhiều tác giả trên thế giới nghiên cứu. Gần đây để đơn giản hóa một số tác giả như Gilbert [9], Long [10]... đã lấy hệ số già cố định bằng 0,8 để tính toán. Tuy nhiên như đã phân tích ở trên, hệ số già là một tham số thay đổi theo thời gian và phụ thuộc vào hàm từ biến của bê tông. Nội dung tiếp theo của bài báo này trình bày các kết quả thiết lập mối quan hệ giữa hệ số từ biến và hệ số già của bê tông theo các cấp cường độ nén bê tông thay đổi, đồng thời tính toán độ võng dài hạn của dầm BTCT dựa theo chỉ dẫn trong tiêu chuẩn EC2 có xét đến hệ số già của bê tông. Các kết quả tính toán được so sánh với kết quả nghiên cứu thực nghiệm tương ứng.
2. Xây dựng mối quan hệ giữa hệ số từ biến và hệ số già
Trong mục này sẽ thiết lập mối quan hệ giữa hệ số từ biến và hệ số già của bê tông, làm cơ sở cho việc tính toán độ võng dài hạn của cấu kiện dầm BTCT.
Theo Bazant [7], hệ số già của bê tông được tính theo biểu thức (1):
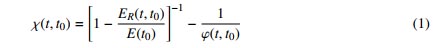
trong đó ER(t; t0) được gọi là hàm chùng (relaxation function), hay là ứng suất tại thời điểm t gây ra bởi một biến dạng đơn vị ở thời điểm t0.
Biến dạng từ biến của bê tông ở thời điểm t bất kỳ được xác định theo công thức (2) như sau:
Ứng suất tương ứng ở thời điểm t được xác định theo công thức (3):
trong công thức (2) và (3): Ɛ0(t) là biến dạng phi tải trọng (gồm biến dạng co ngót và biến dạng nhiệt); Jc(t; t') là hàm từ biến, thể hiện biến dạng ở thời điểm t do ứng suất đơn vị tác dụng ở thời điểm t' gây ra; ER(t; t') là hàm chùng ứng suất, cho biết ứng suất ở thời điểm t gây ra bởi biến dạng đơn vị ở thời điểm t'.
Mối quan hệ giữa các hàm từ biến Jc và hàm chùng ứng suất ER có thể được xác định bằng cách coi lịch sử biến dạng là một hàm đơn vị, đó là Ɛ = 1 khi t ≥ t0 và Ɛ = 0 khi t < t0, trong trường hợp này σ(t) = ER(t; t0). Khi đó, công thức (3) được viết như sau (coi Ɛ0(t) = 0):
khi cho t > t0 ta có:
nếu thay thế
ta có:
Trong các công thức trên, ER(t; t0) được xác định theo công thức (4). Có thể thấy đây là tích phân Volterra và có thể giải bằng cách chia nhỏ thời gian từ t1 đến tn thành các bước thời gian ∆tr [7]. Sử dụng phần mềm giải toán chuyên dụng Matlab để thiết lập chương trình tính cho phép xác định được giá trị ER(t; t0). Mỗi một ER(t; t0) tìm được chỉ tương ứng với một hàm từ biến Jc(t; t0), hay nói cách khác là tương ứng với một cấp cường độ nén của bê tông.
Để tiến hành thiết lập mối quan hệ này, trong nội dung nghiên cứu của bài báo sử dụng các tính toán hệ số từ biến của bê tông theo chỉ dẫn trong tiêu chuẩn EC2 [1] tương ứng với các cấp cường độ nén bê tông là fck = 15 ÷ 35 MPa, độ ẩm môi trường RH = 60%, theo công thức sau:
Trong đó βc(t; t0) là hệ số kể đến sự phát triển từ biến theo thời gian; φ0 là hệ số từ biến danh nghĩa.
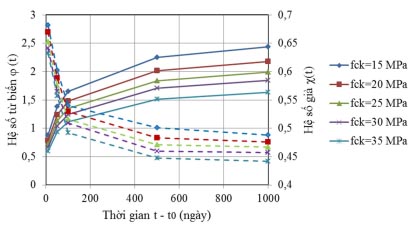
Hình 2. Biểu đồ quan hệ giữa hệ số từ biến và hệ số già của bê tông theo các cấp cường độ nén của bê tông thay đổi.
Các thông số tính toán trên được trình bày chi tiết trong tiêu chuẩn EC 2 [1]. Sau khi xác định được ER(t; t0), thay vào biểu thức (1) để xác định hệ số già χ(t; t0). Trên Hình 2 thể hiện các kết quả tính toán thu được [16, 17].
Kết quả thể hiện trên Hình 2 cho thấy hệ số già của bê tông tỷ lệ nghịch với hệ số từ biến, nghĩa là hệ số từ biến tăng dần theo thời gian còn hệ số già giảm dần theo thời gian. Hệ số từ biến và hệ số già giảm dần khi cường độ nén của bê tông tăng dần. Hệ số già tính trong khoảng thời gian 1.000 ngày, với bê tông có cường độ nén đặc trưng từ 15 MPa đến 35 MPa có giá trị nằm trong khoảng từ 0,4 đến 0,7. Kết quả tính toán này cũng phù hợp với khoảng tính toán mà Bazant [6, 7] và Trost [8] đã công bố là từ 0,4 đến 1,0.
(Còn nữa)
Tài liệu tham khảo
[1] BS EN 1992-1-1 (2004). Eurocode 2: Design of concrete structures, Part 1-1: General - common rules for buildings and civil engineering structures. London: British Standards Institution (BSI).
[2] ACI 318-14 (2014). Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute.
[3] TCVN 5574:2018. Thiết kế kết cấu bê tông và bê tông cốt thép.
[4] Carlsward, J. (2006). ¨ Shrinkage cracking of steel fibre reinforced self-compacting concrete overlays; Test methods and theoretical modelling. Unpublished Doctoral Thesis, Lulea University of Technology, Luleå, Sweden.
[5] Westman, G. (1999). Concrete Creep and Thermal Stresses - New Creep Models and Their Effects on Stress Development. Doctoral Thesis 1999:10, Department of Civil and Mining Engineering, Division of Structural Engineering, Lulea university of Technology, Luleå, Sweden.
[6] Bažant, Z. P. (1972). Numerical determination of long-range stress history from strain history in concrete. Matériaux et Constructions, 5(3):135-141.
[7] Bažant, Z. P. (1972). Prediction of Concrete Creep Effects Using Age-Adjusted Effective Modulus Method. ACI Journal, 69(4):212–217.
[8] Trost, H. (1967). Implications of the Superposition Principle in Creep and Relaxation Problems for Concrete and Prestressed Concrete. Beton-und Stahlbetonbau, (10):230-238. (in German).
[9] Gilbert, R. I., Ranzi, G. (2010). Time-Dependent Behaviour of Concrete Structures. CRC Press.
[10] Long, T. N. (2016). Nghiên cứu thực nghiệm về biến dạng dài hạn cột bê tông cốt thép chịu nén đúng tâm. Luận án tiến sỹ.
[11] CEB-FIP (2010). New Model Code. Final draft, Lausanne Switzerland, Ed Joost Walraven, Convener, fib Special Activity Group 5.
[12] Ghali, A., Favre, R., Eldbadry, M. (2002). Concrete Structures: Stresses and Deformations. E&FN Spon.
[13] Hiếu, N. T., Bình, N. N. (2014). Nghiên cứu thực nghiệm độ võng dài hạn của dầm bê tông cốt thép. Đề tài nghiên cứu khoa học cấp trường Đại học Xây dựng, mã số 75-2014/KHXD.
[14] Bình, N. N., Hiếu, N. T. (2015). Nghiên cứu thực nghiệm độ võng dài hạn của dầm bê tông cốt thép. Tạp chí Khoa học Công nghệ Xây dựng, (23/3).
[15] Hùng, N. M., Phong, N. T., Hiếu, N. T. (2019). Xây dựng mô hình thí nghiệm xác định chùng ứng suất
của bê tông trong kết cấu dầm bê tông cốt thép. Tạp chí Khoa học Công nghệ Xây dựng (KHCNXD) - ĐHXD, 13(4V):1-11.
[16] Hùng, N. M., Linh, N. N. (2019). Một phương pháp biểu diễn chùng ứng suất trong bê tông thông qua hệ số từ biến và hệ số già hóa trong bê tông. Tạp chí Xây dựng Việt Nam, 58(5-2019).
[17] Hùng, N. M. (2021). Nghiên cứu thực nghiệm sự làm việc dài hạn của dầm bê tông cốt thép chịu chuyển vị cưỡng bức gối tựa. Luận án Tiến sỹ.
[18] Minh, P. Q., và cs. (2013). Kết cấu Bê tông cốt thép. Phần cấu kiện cơ bản. Nhà xuất bản Khoa học Kỹ thuật.
VLXD.org (TH/ Tạp chí KHCNXD)




 Sitemap
Sitemap Cá cược game
Cá cược game